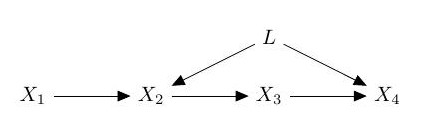
The graph above (which is known as the Verma graph) represents a causal model where X2 is a cause of X4 (via X3) but both X2 and X4 have a common cause L. If L is a latent variable, i.e. not one observed in data, then learning such a causal model is challenging, since we never get to see L! One approach to this difficult learning task is constraint-based learning where an algorithm infers the existence of latent variables from patterns of conditional independence between the observed variables.
An alternative approach is score-based learning where each candidate causal model (including those with latent variables) has a 'score' (typically penalised log-likelihood) and the task is to find a causal model with high (preferably maximal) score. There has been some recent progress in score-based learning for causal models with latent variables much of which has taken advantage of algebraic representations of causal models (see refs). In this existing work only quite small causal models have been learned. The goal of this project would be develop algorithms which can accurately learn larger causal models, even when there are latent variables. Developing algorithms which can incorporate prior knowledge would be advantageous.
When there are latent variables (see project above) learning causal models is particularly hard. If there are no latent variables the problem is easier and so there has been more progress. Nonetheless finding the 'best' directed acyclic graph (DAG) to explain some data is an NP-hard problem so it remains an active area of research.
I have been using integer programming to attack this problem using a system called GOBNILP, which has been used by many other researchers. GOBNILP is built on top of the SCIP constraint integer programming system.(A Python version has also been developed.) The basic idea of this approach is to encode the problem of learning a DAG as a constrained optimisation problem that a solver like SCIP (suitably extended) can solve. This has the advantage that constraints representing prior knowledge (e.g. variable A must/mustn't be a cause of variable B) can be incorporated reasonably easily.
Since DAG learning is NP-hard there is always work to be done, e.g. increasing the size of learning problem where we can (reliably) find an optimal DAG in reasonable time, or handling user-supplied constraints more efficiently. The goal of this project is apply ideas from constraint and integer programming to DAG learning. This will suit someone who likes being able to apply theoretical ideas (from e.g. polyhedral geometry, see 2nd reference below) to design more efficient machine learning software.
There is a growing interest in methods which combine solving combinatorial optimisation (CO) problems and machine learning. In some cases machine learning is used to learn the best strategies for to solving an NP-hard problem. In other cases, CO methods (e.g. integer linear programming (ILP)) are used to solve hard machine learning problems. In yet another combination CO solvers have been included as a layer in a deep learning architecture. The goal of this project is to explore this area further to allow further fruitful cross-fertilisation.